This page is part of a series of posts about what we’ve learned from the LTEE. You can view the original version on Telliamed Revisited.
Endless Adaptations
The bacteria continue to become better and better adapted to the LTEE environment over time, and it appears their fitness may continue to increase indefinitely, albeit at a slower pace.
An exciting new twist on the dynamics of adaptation by natural selection is the discovery that fitness can increase “forever” – or at least for a very long time – even in a constant environment.
A power-law model, which has no upper bound, gives a significantly better fit to the mean-fitness trajectories measured in the LTEE populations than does a model with an asymptote.
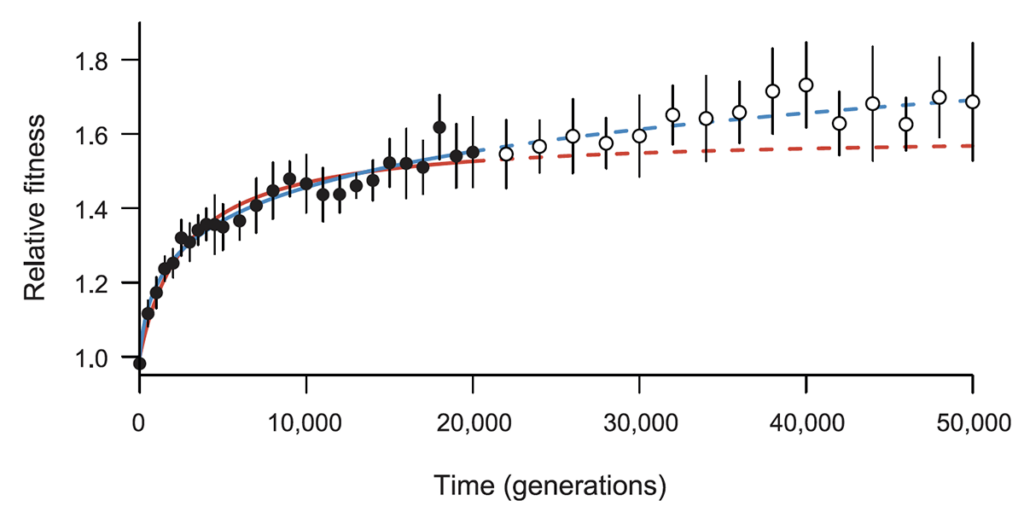
Moreover, the power law predicts the trajectory of fitness evolution with much greater accuracy. That is, if we reduce the data so that it includes only the first 20,000 generations, the power law trajectory that fits this truncated dataset accurately predicts fitness out to 50,000 generations (blue trajectory in the figure below). By contrast, the same procedure with the asymptotic model consistently underestimates the future fitness gains (red trajectory in the figure below).
Also, a dynamical model that incorporates clonal interference (competition between different beneficial mutations) and diminishing-returns epistasis (where the marginal effect of a beneficial mutation declines with increasing fitness) produces trajectories that have the same power-law form. That, in turn, facilitates estimation of important population-genetic parameters including the rate of beneficial mutations and the average strength of the diminishing-returns epistasis.
The figure below shows the grand-mean fitness data (symbols with error bars) over 50,000 generations of the LTEE. It also shows the trajectories predicted by the power law (blue curve) and by a model with an asymptote (red curve) using only the first 20,000 generations of data. The figure comes from Wiser et al., 2013, Science; it is shown here under the doctrine of fair use.