Skip to content

What We’ve Learned about Evolution from the LTEE: Number 5

Print

This page is part of a series of posts about what we’ve learned from the LTEE. You can view the original version on Telliamed Revisited.

Changing Mutation Rates

Several LTEE lines have evolved large changes in their spontaneous mutation rates, reflecting a tradeoff between short-term fitness and long-term evolvability

We have seen large changes in the spontaneous mutation rate in some of the LTEE populations.  These changes reflect an interesting tradeoff between short-term fitness and long-term evolvability.

Proximate causes.  Six of the 12 LTEE populations evolved to be so-called “hypermutators” by 50,000 generations.  The proximate (i.e., biochemical) causes of these changes are mutations in genes whose products are involved in DNA repair or the degradation of molecules that cause damage to DNA.

These mutations typically cause the rate of point mutations throughout the genome to increase by roughly 100-fold (Sniegowski et al., 1997, Wielgoss et al., 2013), so their effects are not at all subtle.  They also change the spectrum of mutations:  mutations in the mutS gene, which encodes a protein involved in mismatch repair, cause increased A·T–>G·C and G·C–>A·T transitions (Lenski et al., 2003); while mutations in mutT, which encodes an enzyme that degrades an oxidized nucleotide, cause A·T–>C·G transversions (Barrick et al., 2009).

Evolutionary effects.  The evolutionary effects of these hypermutators are subtle and interesting.  In essence, one can think of mutations that produce hypermutators as affecting the tradeoff between short-term fitness and long-term evolvability.

Short-term cost.  Of all the possible mutations that might occur, many more are deleterious than are beneficial. Therefore, hypermutators produce more maladapted progeny than otherwise identical cells with a lower mutation rate.  Hence, hypermutators suffer a fitness cost caused by the increased production of progeny with deleterious mutations.

However, the E. coli strain that was the ancestor to the LTEE has a low point mutation rate, which we’ve estimated as ~10-10 per base-pair per generation (Wielgoss et al., 2011).  Given the genome contains ~5 x 106 base-pairs, this rate translates to only ~0.0005 point mutations per genome per generation.  Therefore, even a 100-fold increase means that most hypermutator progeny are mutation-free.  Considering that only a fraction of genomic sites are subject to mutations that would be deleterious in the LTEE environment, we infer that the short-term cost to a 100-fold hypermutator is ~1% (Wielgoss et al., 2013).

Evolvability benefit.  Even a 1% cost is not trivial, so how can a hypermutator survive and spread through a population?  In fact, most hypermutators do not survive; the vast majority of mutations that cause hypermutators will die out as a consequence of that short-term cost.  However, hypermutators result from loss-of-function mutations, and a dozen or so large genes are targets for these mutations.  Hence, new hypermutators will continually be regenerated in large populations.  Absent other forces, an equilibrium frequency of hypermutators would be reached that reflects the balance between the rate of appearance of hypermutators by new mutations in the relevant genes and the rate at which they are removed by selection against the deleterious mutations they cause—in other words, the familiar mutation-selection balance of population-genetics theory.

But another force is at play: the populations in the LTEE are not sitting on a fitness peak, so there are on-going opportunities for beneficial mutations to appear.  And a hypermutator cell has a much higher probability of generating a beneficial mutation than does a “normal” cell.  In essence, there’s a race to produce the next winner.  If a hypermutable cell generates the next beneficial mutation that sweeps through the population, then the hypermutator will “hitchhike” along with it because, without sex, the two mutations are linked.

Combining forces.  So how do the short-term cost and the evolvability benefit play out together?  Mutations that knock out any one of the genes involved in DNA repair probably occur at a rate between 10-5 and 10-6 per generation, and the resulting hypermutable cells have a fitness disadvantage of ~1% owing to the production of deleterious mutations.  At mutation-selection balance, the frequency of hypermutators is between 0.01% (10-4) and 0.1% (10-3).  Let’s use 0.05% to illustrate.

Although the hypermutators are a small minority, on a per capita basis each of them has a 100-times higher probability than a normal cell of generating the next winner.  So 5% of the time, a hypermutator will be swept to fixation, but most of the time the winner will be produced by a normal cell.  Now consider the fact that each of the LTEE populations has had many beneficial mutations go to fixation over its history.  After 14 selective sweeps, the odds are better than 50:50 that at least one of those beneficial mutations was generated by a hypermutator.

King of the mountain.  After a hypermutator becomes common, it becomes very hard to dislodge it from the population.  This difficulty follows from the same logic as above.  Once the hypermutator reaches 1% of the population, it has a 50% chance of generating the next winner; by the time it gets to a 50% frequency, the odds are 100:1 in its favor.  Thus, a hypermutator only needs to get lucky once, and then it becomes extremely difficult to displace it … at least so long as the population is far from the fitness peak.

Nothing lasts forever.  Even before a population reaches a fitness peak, its rate of fitness improvement typically decelerates, at least in a constant environment like that of the LTEE (Wiser et al., 2013).  At some point, the magnitude of the benefit that would result from reducing the mutation rate and its associated fitness cost may become commensurate with the fitness advantages that are available from other mutations.  When that happens, selection to reduce the mutation rate becomes effective, and the hypermutable “king of the mountain” can be displaced by a genotype with a lower mutation rate.

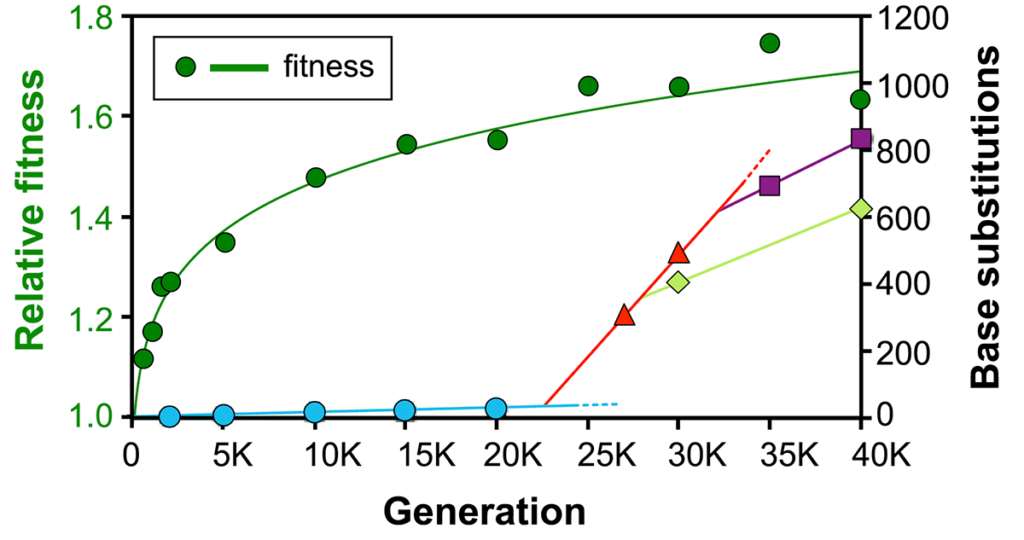
Indeed, we have observed this displacement occurring in one of the LTEE populations (Wielgoss et al., 2013).  In that population, not one but two lineages independently arose (see Figure below) that reduced the mutation rate by about half, while reducing the fitness cost from ~1% to ~0.5%.  The population thus remains hypermutable, but less so than before.

What the future may hold.  In that paper, we hinted that it is probably easier to reduce the mutation rate in stages rather than to revert to the ancestral rate in a single step.  That’s because the population is continuing to adapt, albeit at a slower rate.  A genotype with a 50% reduction in the mutation rate will save half of the fitness cost of the full-blown hypermutator, yet it will continue to produce 50 times as many other beneficial mutations as would a genotype that reverted to the ancestral mutation rate.  In essence, the fitness costs and the evolvability benefits are on very different scales.

The figure below shows the decelerating fitness trajectory (dark green curve, left axis) and the number of mutations (right axis) as the lineage with the ancestral mutation rate (blue) is replaced by a hypermutator lineage (red), which in turn is displaced by two independent lineages with somewhat lower mutation rates (light green and purple).  The figure comes from Wielgoss et al., 2013, Proc. Natl. Acad. Sci. USA; it is shown here under the doctrine of fair use.